Research Overview
My research centers around improving the accuracy and efficiency of numerical methods that model geophysical fluid dynamics by removing errors from the following:
Spatial Representation of geophysical fluid domains within a computer.
This requires automatically extracting topological features such as distances, boundaries, gradients, and local feature sizes from satellite and observational data to create a geometrical representation of the fluid domain under consideration. From this representation, we construct a numerical mesh function and utilize a force displacement method to automatically create a high quality simplex mesh. This mesh then serves as the numerical domain over which we solve the differential equations that model fluid dynamics.
Numerical Solution Method.
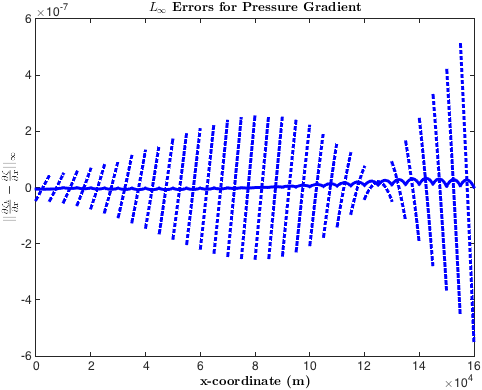
A significant portion of my research focuses on developing high resolution numerical methods for fluid flow and transport. The methods center around novel discontinuous Galerkin (DG) finite element methods that preserve the natural coupling of dynamical systems. For instance, three-dimensional shallow flow requires the solution of a system of differential equations that are highly-coupled—any low order approximation will propagate through the entire solution smoothing out gradients and diffusing mass—producing incorrect transport patterns. We alleviate this is issue with high-order integration methods that accurately determine pressure gradients that drive fluid flow.
Errors in the pressure gradient calculation. The blue dashed line corresponds to errors in the typical pressure calculation while the solid blue line corresponds to errors produced by our high-order methods.
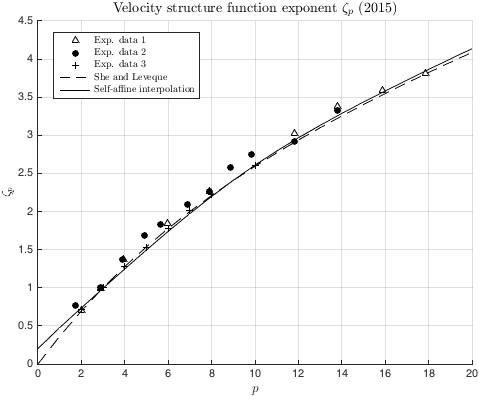
Velocity structure function exponents. Black solid line corresponds to our interpolation method while the black dashed line corresponds to the theory of She and Leveque ('95). Experimental data is from Anselmet et al. ('84) and Benzi et al. ('93).
Physical Understanding.
The chaotic nature of turbulence has baffled scientists since it was highlighted by Osborne Reynolds in 1926. While laminar flow is smooth, turbulence is rugged and rough; we approximate its geometry with self-affine fractals and moment field equations. Applications include air-sea turbulence, where high-frequency gravity waves in the atmosphere create high-frequency gravity waves in the sea-surface through pressure perturbations in their interface.